数字基础

当我们还是孩子的时候，我们就用数字来表示数量。这对我们来说似乎是天经地义的，但是对一个古罗马人来说却未必如此。对他们来说，每个用来表示数字的符号总是代表相同的值:

I      1
II     2
III    3
IV     4
V      5

所有的I符号无论在哪里都表示值1(1)，而V符号总是表示值5(5)。然而，这在我们的十进制系统中是不存在的。当我们写数字1时，我们并不总是表示1的值(罗马数字中的I)。例如:

  1    I
 10    X
100    C

所以，符号1并不总是值为1(或罗马数字中的I)。例如，在第二种情况中，符号1表示10的值(罗马语为X)，在第三种情况中，1表示100的值(罗马语为C)。

例如:

275不等于2+7+5，可以分解为200+70+5:

因此，第一个“2”相当于200 (2 x 100)，第二个“7”相当于70 (7 x 10)，而最后一个"5"对应的值是5 (5 x 1)。

这是因为我们的系统是一个位置数字系统。因此，给定数字的值取决于它在所表示的整个数字中的位置。所有这些都可以用一种非常简单的方法在数学上表示出来。例如，为了表示值182736，我们可以假设每一位数字都是自身乘以10的指数位，从右边开始是10⁰，接着是10¹、10²，以此类推:

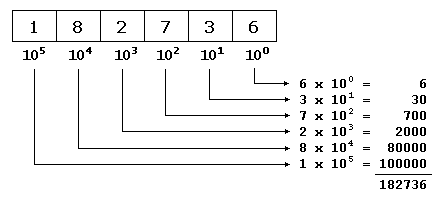
☲ 八进制数(以8为基数)

就像我们的“正常”数字是以10为基数(或基数10)，因为我们有10个不同的数字(从0到9):

0123456789

八进制数字只包括0到7的值的表示:

01234567

因此，它的数学基数是8。在c++中，八进制数总是以0开始表示。八进制这样来表示第一个数字:

八进制  十进制
-----  -------
  0       0
 01       1
 02       2
 03       3
 04       4
 05       5
 06       6
 07       7
010       8
011       9
012      10
013      11
014      12
015      13
016      14
017      15
020      16
021      17

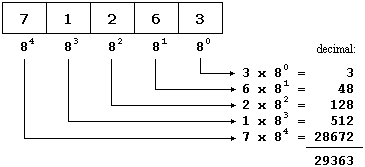
例如，数字17(17或罗马数字XVII)在c++中表示为八进制数021。我们可以将之前对十进制数的处理方法应用到八进制数上，只需要考虑它的底数是8。
例如，取八进制数字071263:

因此，八进制数071263表示为十进制数29363。

☲ 十六进制数(以16为基数)

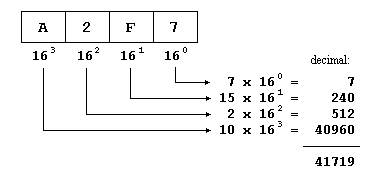
像十进制数有10个不同的数字代表(0123456789)和八进制数字8(01234567), 十六进制数字有16个不同的数字,所代表的数字从0到9,以及字母A, B, C, D, E和F 16个不同的符号,表达我们需要的基本16个数字:

十六进制  十进制
-----  -------
      0         0
    0x1         1
    0x2         2
    0x3         3
    0x4         4
    0x5         5
    0x6         6
    0x7         7
    0x8         8
    0x9         9
    0xA        10
    0xB        11
    0xC        12
    0xD        13
    0xE        14
    0xF        15
   0x10        16
   0x11        17

在c++中，十六进制数前有0x (0, x)。同样，我们可以使用相同的方法将一个数从基数转换为另一个数:

☲ 二进制

八进制数和十六进制数在比特世界中比十进制数有很大的优势，它们的基数（8和16）是2的完美倍数（分别为2³和2⁴），这使得我们可以更容易地从这些基数转换为二进制数，而不是从十进制数（基数为2x5）转换为二进制数。例如，假设我们要将以下二进制序列转换为其他基数的数字：

110011111010010100

为了将它转换为十进制，我们需要进行一个数学运算，类似于我们以前使用的从十六进制或八进制转换的运算，这将得到十进制数212628。

然而，将这个序列传递给八进制只会花费我们几秒钟的时间，即使是不太擅长数学的人也可以通过观察来完成:因为8是2³，我们将二进制值分成3个数字组:

110 011 111 010 010 100

现在我们只需要将每一组分别转换为八进制基数:

110 011 111 010 010 100
 6   3   7   2   2   4

结果是637224。同样的过程也可以反向执行以从八进制转换到二进制。
为了对十六进制数进行运算，我们只需要执行相同的过程，但将二进制值分成4个数字组，因为16 = 2⁴:

11 0011 1110 1001 0100
3    3    E    9    4

因此，二进制表达式110011111010010100可以用c++表示为212628(十进制)、 0637224(八进制)或0x33e94(十六进制)。

十六进制在计算机科学中非常有用，因为现在计算机是基于8个二进制位组成的字节，因此每个字节都与2个十六进制数字所能代表的范围相匹配。由于这个原因，它经常被用来表示转换成二进制或从二进制转换.